Die Animationen werden durch einen Klick auf die Bilder gestartet.
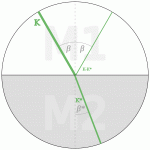
Goethes These von der Polarität zwischen Helligkeit und Dunkelheit hat scharfe empirische Konsequenzen. Hier ein Beispiel mit Animation für versierte Physkerinnen und Physiker. Trifft ein Lichtstrahl mit Beleuchtungsdichte K im Winkel ß auf eine Grenze zwischen zwei Medien M1 und M2 (z.B. zwischen Luft und Glas), so dringt er partiell ins Medium M2 ein, und zwar mit Beleuchtungsdichte K*<K (wobei dieser Anteil – wegen der Refraktion – im veränderten Winkel ß* weiterreist). Der Rest der ursprünglichen Beleuchtungsdichte (K-K*) wird mit Ausfallswinkel ß ins Medium M1 reflektiert.
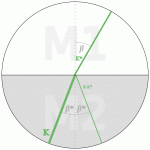 Nun gilt aus Gründen der Symmetrie für einen zweiten Lichtstrahl, der umgekehrt im Einfallswinkel ß* von M2 nach M1 zur Mediengrenze reist und partiell in den refrangierten Pfad des ersten Lichtstrahls reflektiert wird: Dieser zweite Lichtstrahl wird partiell in den reflektierten Pfad des ersten Strahls refrangiert; soweit ist die Sache einfach.
Nun gilt aus Gründen der Symmetrie für einen zweiten Lichtstrahl, der umgekehrt im Einfallswinkel ß* von M2 nach M1 zur Mediengrenze reist und partiell in den refrangierten Pfad des ersten Lichtstrahls reflektiert wird: Dieser zweite Lichtstrahl wird partiell in den reflektierten Pfad des ersten Strahls refrangiert; soweit ist die Sache einfach.
Aber die von Goethe entdeckte Polarität zieht folgende Forderung nach sich: Falls der zweite Lichtstrahl ursprünglich ebenfalls mit Beleuchtungsdichte K ausgestattet war, wird er exakt mit Beleuchtungsdichte (K-K*) reflektiert und mit Beleuchtungsdichte K* transmittiert. D.h. die Summe der Beleuchtungsdichten ist in dieser Konfiguration auf allen betrachteten Pfaden konstant. Ich erschrak, als mir im Gespräch mit Matthias Rang klar wurde, dass Goethes 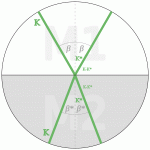 Polarität eine so scharfe empirische Bedingung nach sich zieht. Matthias Rang hat die Sache später mithilfe der Formeln Fresnels nachgerechnet (die für völlig andere Probleme geschaffen wurden); und gespenstischerweise ging die Rechnung exakt auf.
Polarität eine so scharfe empirische Bedingung nach sich zieht. Matthias Rang hat die Sache später mithilfe der Formeln Fresnels nachgerechnet (die für völlig andere Probleme geschaffen wurden); und gespenstischerweise ging die Rechnung exakt auf.