< Zurück | Übersicht der Farbtafeln | Weiter >
 | Newtons Vollspektrum: Dies Spektrum bezeichne ich nur dann als Vollspektrum, wenn ich es ausdrücklich von anderen Spektren unterscheiden möchte, in denen weniger Farben vorkommen; solange es darauf nicht ankommt, rede ich oft einfach nur von Newtons Spektrum. Von oben nach unten sieht man Blau, Dunkeltürkis, Grün, Dunkelgelb, Rot, mit fließenden Übergängen. Insgesamt wirken die Farben vergleichsweise dunkel; das fällt besonders beim Gelb und Türkis auf. Dies Photo wurde nicht mit Sonnenlicht, sondern mit dem ähnlich zusammengesetzten Licht eines Diaprojektors erstellt; das Ausgangsbild war nicht rund (wie bei der Sonnenscheibe), sondern ein schmaler horizontaler Lichtbalken. |
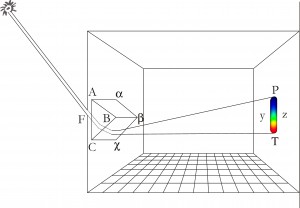 | Newtons Grundexperiment: Ein Sonnenstrahl wird durchs Fensterladenloch F in ein Glasprisma ABCαβχ geschickt; an beiden Grenzflächen des Prismas wird er gebrochen (refrangiert), und zwar zunächst an der Fläche AαχC zum Lot hin (beim Übergang vom optischen dünnen Medium Luft zum optisch dichten Medium Glas) und danach an der Fläche BβχC vom Lot fort (beim Übergang von Glas in Luft). Die beiden Brechungen führen zu einer erheblichen Ablenkung vom geraden Weg, und zwar nach oben, wobei der ursprünglich weiße Lichtstrahl in seine kunterbunten Bestandteile zerlegt wird: Auf der Rückwand der Dunkelkammer zeigt sich das newtonische Vollspektrum aus den dunklen Farben Blau/Türkis/Grün/Gelb/Rot. Das Spektrum ist ca. fünfmal so lang wie breit. |
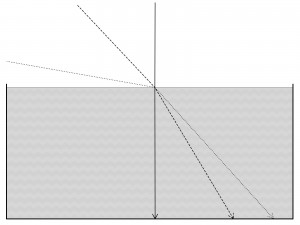 | Lichtbrechung an einer Wasseroberfläche: Der gepunktet eingezeichnete Lichtstrahl trifft von links sehr flach auf die Wasseroberfläche, wird hin zum Lot gebrochen und ändert seine Reiserichtung besonders stark. Der gestrichelt eingezeichnete Lichtstrahl trifft weniger flach aufs Wasser; er wird ebenfalls zum Lot hin gebrochen, ändert seine Reiserichtung aber weniger stark. Der durchgezogene Lichtstrahl trifft senkrecht aufs Wasser; er ändert seine Reiserichtung am allerwenigsten – gar nicht. |
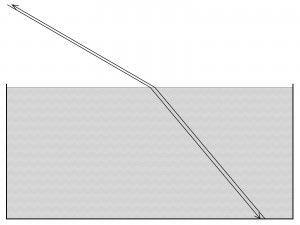 | Lichtbrechung im Vorwärts- und im Rückwärtsgang: Die Geometrie eines gebrochenen Lichtstrahls hängt nicht von der Reiserichtung ab. Der rechts unten entspringende Lichtstrahl (der vom Boden des Aquariums ausgeht) wird beim Übergang ins weniger dichte Medium vom Lot weg gebrochen; er reist auf demselben Pfad wie sein gegenläufiger Kollege (von links oben). Die Reisen der beiden unterscheiden sich nur in der Richtung. Deckungsgleiche Pfade sind in der Abbildung durch eng parallel geführte Pfade angedeutet. |
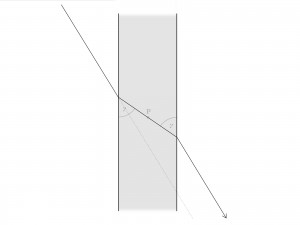 | Lichtbrechung an einer Fensterscheibe: Bei zweifacher Brechung an planparallelen Mediengrenzen wie z.B. einer Fensterscheibe heben sich die beiden Richtungsänderungen gegenseitig auf; im Ergebnis reist der Lichtstrahl am Ende in der ursprünglichen Richtung weiter (nur parallel nach oben verschoben, im Vergleich zur gestrichelt angedeuteten Fortsetzung des nicht gebrochenen Strahls). Der Grund: Der Lichtstrahl im Innern der Fensterscheibe bildet links und rechts zu den Medieninnengrenzen identische Winkel β (sogenannte Z-Winkel). Da es auf die Reiserichtung nicht ankommt, muss die Situation jenseits der linken Mediengrenze mit derjenigen jenseits der rechten Mediengrenze übereinstimmen. Es herrscht Punktsymmetrie, und zwar zu einem Punkt P auf dem Lichtpfad, der exakt in der Mitte der Fensterscheibe liegt. |
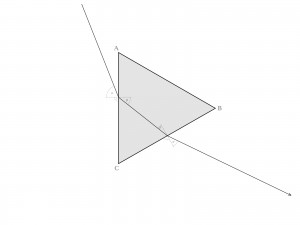 | Lichtbrechung am Prisma: Ein Lichtstrahl trifft von links oben aufs Prisma und wird an beiden Mediengrenzen AC und BC nach links vom Weg abgelenkt: Bei der ersten Brechung hin zum gepunktet angedeuteten Lot, bei der zweiten Brechung vom gestrichelt angedeuteten Lot fort. Zusammengenommen führen die beiden Effekte dazu, dass man mit einem Prisma förmlich um die Ecke gucken kann – vor allem bei Prismen aus Glas mit extrem hoher Brechzahl. |
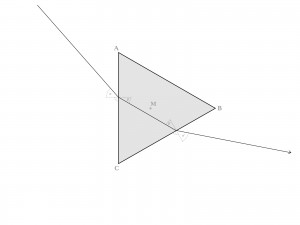 | Strahlengang im symmetrisch ausgerichteten Prisma: Wer das Prisma ABC um seine Achse in M rotieren lässt, kann mit etwas Geduld eine besondere Position finden, in der die doppelte Refraktion insgesamt minimal wird. Das ist dann der Fall, wenn Eintritts- und Austrittswinkel des Lichtstrahls identisch sind; dann gilt α = α' und β = β'. Bei dieser besonderen Ausrichtung des Prismas herrscht Symmetrie entlang der Achse CM; und im Innern des Primas verläuft der Lichtstrahl parallel zu dessen Grundfläche AB. |
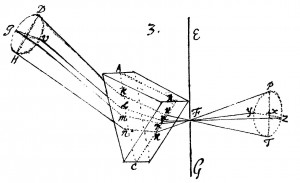 | Originalskizze aus Newtons Vorlesungsmanuskript: Wie Newton kontrafaktisch zeigen will, würden Lichtstrahlen gleicher Refrangibilität ein rundes Bild der Sonne in der Dunkelkammer erzeugen, selbst nach dem Durchgang durchs Prisma. Hierfür reduziert Newton die geometrische Komplexität in seinem Grundexperiment; u.a. nimmt er an, dass (i) das Fensterladenloch F unendlich klein ist und dass (ii) das Sonnenbild PZTY genau gegenüber vom Fensterladenloch auf die Dunkelkammerrückwand fällt. Mit einem beweglichen Schirm (den man kippen kann) ließe sich Annahme (ii) leichter realisieren. |
 | Bildverschmutzungen infolge chromatischer Aberration: Hier blicken Sie durchs Prisma (links im Bild) auf die sauberen Schachfiguren (rechts). Wegen der Refraktion am Prisma können Sie sozusagen um die Ecke schauen. Im Prisma zeigen sich beide Schachfiguren in voller Größe – aber leider mit unscharfen Rändern. Schuld daran ist die chromatische Aberration: Das heterogene Licht, das von der weißen Königin und von der grauen Ebene durchs Prisma ins Auge reist, wird je nach Farbe verschieden weit gebrochen. Ein genauer Blick auf die unscharfen Figurgrenzen zeigt die türkis/blauen bzw. rot/gelben Farbsäume, die für den Effekt verantwortlich sind. (Die abgeschnittenen Figurfragmente, die sich rechts im Prisma zeigen, sind dagegen völlig scharf; sie beruhen auf Spiegelungen am Prisma). Auch an jeder Linse aus homogenem Material lässt sich die chromatische Aberration beobachten. |
< Zurück | Übersicht der Farbtafeln | Weiter >